LC-Meter – DL8NCI

0. Vorbemerkungen

Dieser Artikel beschreibt einen Prototyp eines LC-Meters und vor allem die dahinter stehende Theorie. Eine praktische Bauanleitung incl. Platine und Stückliste ist im Artikel LC-Meter 2.0 beschrieben.

1. Motivation

Vor einiger Zeit hat mich die Frage eingeholt, wie gross denn wohl die Induktivität einer unbekannten Spule ist. Oder etwas genauer gefragt: wie gross ist der Kopplungsfaktor zweier Wicklungen auf einem Ringkern, den ich als Balun von 50 Ohm unsymmetrisch auf 50 Ohm symmetrisch benutzen wollte.

Ein Balun — Beispiel für eine Induktivität, die aus drei gleichartigen Wicklungen auf einem Ringkern besteht.

Dazu kann man die zwei Wicklungen auf dem Ringkern (im Bild sind es tatsächlich drei Wicklungen; die gerade nicht betrachtete Wicklung kann jeweils ignoriert werden) wie die zwei Wicklungen eines Transformators betrachten. Ich nenne sie daher auch Primär- und Sekundärwicklung. Selbst dann, wenn wie in meinem Fall, Primär- und Sekundärwicklung gleichartig aufgebaut sind, und sie vertauschbar sind.

Um nun den Kopplungsfaktor zwischen zwei Wicklungen, die sich auf einem Wickelkörper befinden, zu bestimmen, lautet eine mögliche Meßvorschrift wie folgt:

1.1 Erste Messung: Serienschaltung der Induktivitäten

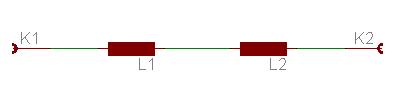
Messe die Induktivität, wenn die Primärwicklung und die Sekundärwicklung in Reihe geschaltet sind. Diesen Wert nennen wir L_x. Das heißt, der Anfang der Primärwicklung wird mit dem einen Anschluß des Induktivitätsmeßgerätes verbunden. Das Ende der Primärwicklung wird mit dem Anfang der Sekundärwicklung verbunden. Das verbliebene Ende der Sekundärwicklung verbindet man mit dem anderen Pol des Meßgerätes. Wenn Primär und Sekundärwicklung gleichartig aufgebaut sind, so ist die Induktivität der Reihenschaltung etwa das vierfache einer einzelnen Wicklung, da die Induktivität
proportional zum Quadrat der Windungszahl ist: Doppelte Windungszahl, vierfache Induktivität; dreifache Windungszahl, neunfache Induktivität; usw. Diese Aussage gilt natürlich nur bei starker Kopplung, wie sie in Transformatoren und auf meinem Ringkern zu erwarten ist. Bei sehr schwacher Kopplung würden sich die Induktivitäten der beiden Wicklungen einfach addieren. Das wäre beispielsweise bei zwei Festinduktivitäten oder bei zwei Spulen, die genügend weit voneinander entfernt sind, der Fall. In der Praxis wird man viele Fälle finden, bei denen die Gesamtinduktivität zwischen der doppelten (keine Kopplung) und der vierfachen Induktivität (perfekte Kopplung) liegt.

1.2 Zweite Messung: Anti-Serienschaltung der Induktivitäten

Anti-Serienschaltung zweier Induktivitäten

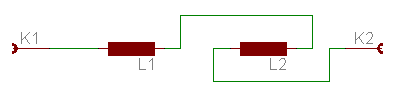
Messe die Induktivität, wenn gegenüber der ersten Messung eine der beiden Wicklungen umgepolt wird. Diesen Wert nennen wir L_y. Bei starker Kopplung und ansonsten gleichartigen Wicklungen erhält man das, was man eine bifilar gewickelte Spule bezeichnet. Die Konsequenz ist, daß die resultierende Induktivität nahe bei Null liegt. Zumindest ist sie sehr klein verglichen mit den Induktivitäten der einzelnen Wicklungen. Wenn gar keine Kopplung vorliegt, dann addieren sich ebenfalls die einzelnen Induktivitäten. Genauso, als ob man zwei Festinduktivitäten auf dem Labortisch liegen hat, die in Reihe geschaltet sind, und von denen man eine umpolt. Die Gesamtinduktivität ändert sich nicht.

1.3 Auswertung

Aus der Messung der Induktivität für die Serienschaltung $L_x$ und der Induktivität für die 'Anti-Serienschaltung' $L_y$ sowie der Messung der einzelnen Induktivitäten $L_1$ und $L_2$ kann der Kopplungsfaktor $k$ wie folgt ermittelt werden:

(1) $\begin{equation*} k = \frac{L_x - L_y}{4 \cdot \sqrt{L_1 \cdot L_2}} \end{equation*}$

Kennt man übrigens den Kopplungsfaktor $k$ , so läßt sich die Gegeninduktivität $M$ wie folgt berechnen:

(2) $\begin{equation*} M = k \cdot \sqrt{L_1 \cdot \L_2} \end{equation*}$

Wenn man zwei Induktivitäten hat, für die $L_1 = L_2$ ist und die nicht gekoppelt sind (z.b. jede Induktivität auf einem eigenen Ringkern), dann ist $L_x = L_y$ und somit $k = 0$ und $M = 0$ . Befinden sich dagegen diese zwei gleichen Induktivitäten gemeinsam auf einem Ringkern - was eine sehr starke Kopplung bewirkt - dann ist $L_x = 4 \cdot L_1 = 4 \cdot L_2$ und $L_y = 0$ . Durch einsetzen in die erste Gleichung erhält man $k = 1$ und somit $M = L_1 = L_2$ . Je nach Konstruktion kann man losere Kopplungen (zwei Luftspulen ein einem gewissen Abstand) oder festere Kopplungen (ein Netztransformator) erhalten. Man kann die Kopplung als ein Maß verstehen, das angibt, wie stark das Magnetfeld der einen Induktivität das Innere der jeweils anderen Induktivität durchdringt.

Weitere Anwendungen zum LC-Meter werden hier vorgestellt.

Festlegung eines Konzeptes

Da ich gerade kein Induktivitätsmeßgerät zur Hand hatte, habe ich mir eins gebaut. Na ja … es ist ein kleines Projekt draus geworden. Im Web findet man natürlich immer Anregungen. Und letztlich unterscheidet sich meine Lösung nicht fundamental von der Lösung in [1].

Grundsätzlich wird (zumindest in meinem Projekt) die Bestimmung der Induktivität L auf die Frequenzmessung eines freischwingenden Oszillators zurückgeführt, wobei die Thomsonsche Schwingungsformel

(3) $\begin{equation*} \omega = 2 \pi f = \frac{1}{\sqrt{L C}} \end{equation*}$

die Frequenz $f$ oder die Kreisfrequenz $\omega$ mit der unbekannten Induktivität $L$ und der bekannten Kapazität $C$ des Schwingkreises verknüpft.

Eine alternativer Ansatz besteht aus einem Oszillator, der lose an den Schwingkreis gekoppelt ist, der wiederum die zu messende Induktivität $L$ enthält. Gemessen wird die Spannung $U(f)$ über dem Schwingkreis in Abhängigkeit von der Frequenz $f$ . Stimmt die Frequenz des Oszillators mit der Eigenfrequenz des Schwingkreises überein, so ist die Spannung maximal. Die Induktivität wird auch hier über die Thomsonsche Schwingungsformel errechnet. Letzten Endes handelt es sich hier direkt um die Aufnahme der Resonanzkurve.

Eine dritte Variante beruht auf der Wheatstone'schen Wechselstrom-Brücke. Ich möchte sie hier nicht weiter betrachten.

Aus diesen Vorbemerkungen ergeben sich folgende Anforderungen

Das LC-Meßgerät muß sowohl sehr kleine Induktivitäten (kleiner 1 μH) als auch sehr große Induktivitäten (nicht unter 100 mH) messen können.
Das LC-Meßgerät muß in der Lage sein, Kapazitäten aufgrund des Layouts und des Oszillators zu ermitteln und bei der Berechung der Induktivität zu berücksichtigen. Diese Forderung ist gleichbedeutend mit dem Wunsch, auch unbekannte Kapazitäten messen zu können.
Eine zum vorigen Punkt verwandte Forderung ist, daß eineInduktivität bereits einen Kondensator parallel geschaltet haben darf, der die L-Messung nicht beeinträchtigt.
Idealerweise sollte die Induktivitätsmessung direkt oder indirekt auf eine Widerstandsmessung zurückgeführt werden. Grund ist vor allem, daß man nicht an jeder Straßenecke Induktivitäten mit geringer Toleranz und hoher Langzeitstabilität beschaffen kann. Bei Kondensatoren ist die Situation schon besser - Kondensatoren mit 2,5% Toleranz sind durchaus im einschlägigen Versandhandel erhältlich. Noch geringere Toleranzen sind bei Widerständen möglich - vor allem, wenn sie für Meßzwecke ausgelegt wurden (0,1%).

**Bild 2:** Das Prototyp- und Experimentierboard des LC-Meßgerätes. Vorne links befindet sich der LC-Oszillator, hinten links der monostabile Multivibrator. In der rechten Hälfte dominiert der ATMega163. Hinten rechts befindet sich der Anschluß des LC-Displays und hinten in der mitte erkennt man den Spannungsregler, dessen Kühlkörper etwas groß geraten ist. Die Verbindungen mit dem Controller erfolgt über Steckbrücken.

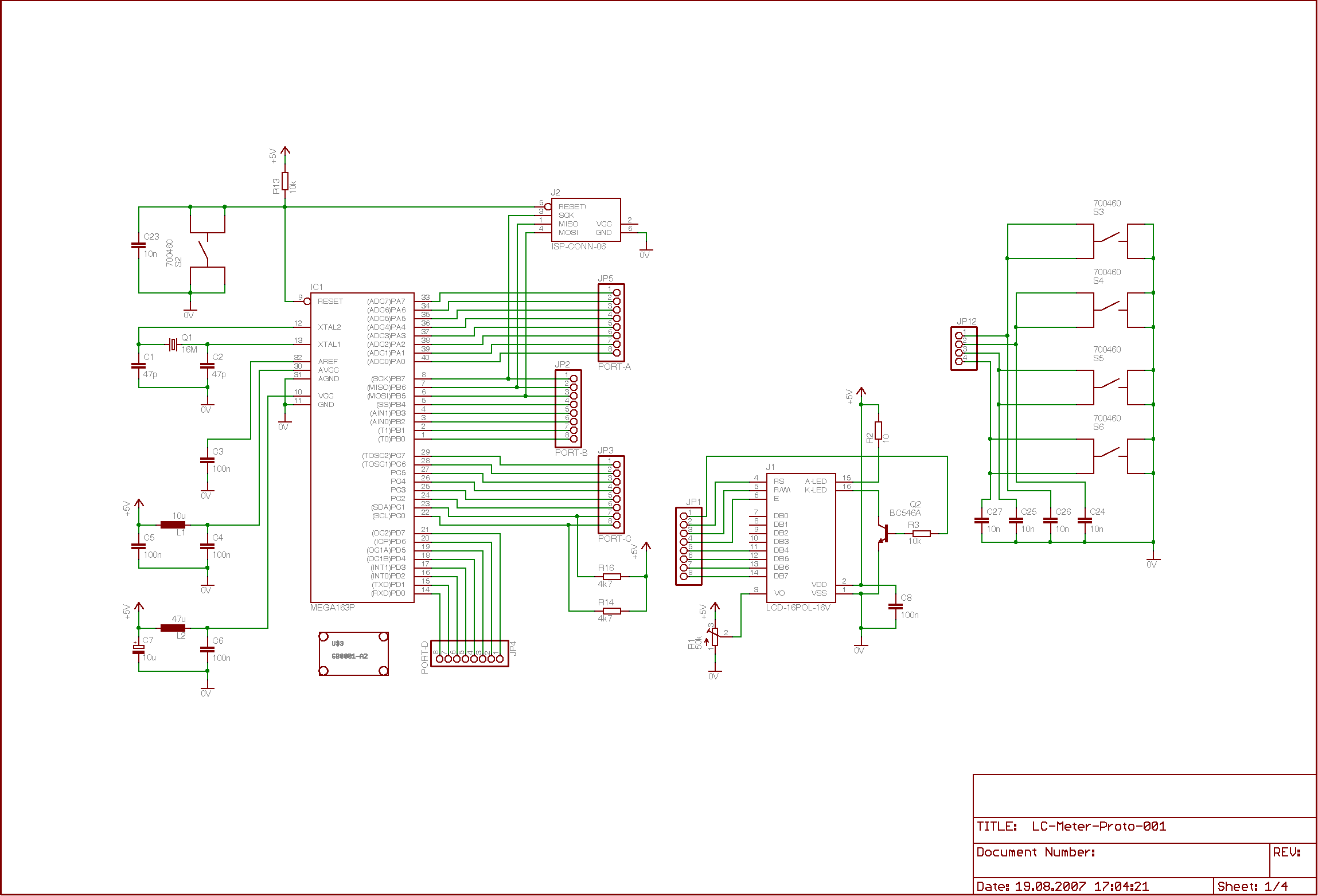
3. Blockschaltbild

Das LC-Meßgerät besteht aus folgenden Baublöcken:

LC-Oszillator mit LM311 ([5])
Monostabiler Multivibrator mit NE555 ode LM555 ([6])
Atmel ATMega163 RISC-Prozessor ([2])
LC-Display
Bedienelemente

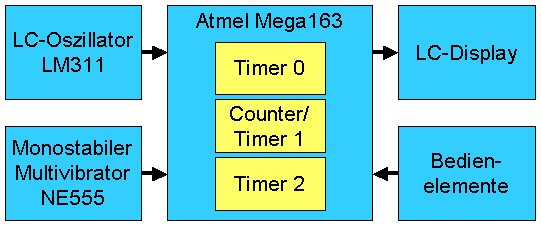
**Bild 3:** Die wesentlichen Komponenten des LC-Meßgerätes

Die wesentliche Baugruppe ist der freischwingende LC-Oszillator. Sein frequenzbestimmender Schwingkreis besteht aus der zu messenden Induktivität L und der Kapazität C, die als bekannt angenommen wird. Als aktives Bauelement findet der Komparator LM311 Verwendung.

Nicht minder wichtig ist der Micro-Controller ATMega163 von Atmel. Der ATMega163 ist zwar mittlerweile veraltet und kann leicht durch einen ATMega16 oder, falls nötig, durch den größeren ATMega32 oder deren Nachfolger ersetzt werden. Ich hatte einen 163er noch in der Schublade gehabt und wollte ihn in diesem Projekt einem sinnvollen Verwendungszweck zuführen. Der ATMega163 enthält eine Reihe verschiedener peripherer Komponenten, von denen neben den klassischen I/O-Ports die drei kombinierten Timer und Counter für das LC-Meter mit die wichtigsten sind.

Das LC-Display dient als Ausgabemedium. Im Prototyp wir ein vierzeiliges Exemplar eingesetzt. Für die tägliche Anwendung dürfte wohl ein zweizeiliges Display vollkommen ausreichen.

Bedient wird das LC-Meter mittels einiger weniger Taster. Neben einem Taster, der die Hintergrundbeleuchtung des LCD schaltet, gibt es einen weiteren, der den Meßmodus
(L-Messung, C-Messung über den Oszillator, C-Messung mit dem NE555) bestimmt.

Abschließend gibt es noch den monostabilen Multivibrator, der mit einem NE555 aufgebaut ist. Er dient dazu, die Kapazität über die Zeit, die benötigt wird, einen Kondensator über einen Widerstand aufzuladen, zu ermitteln. Hier steht die Idee im Vordergrund, die Kapazitätsmessung, wie eingangs gefordert, auf eine Widerstandsmessung zurückzuführen.

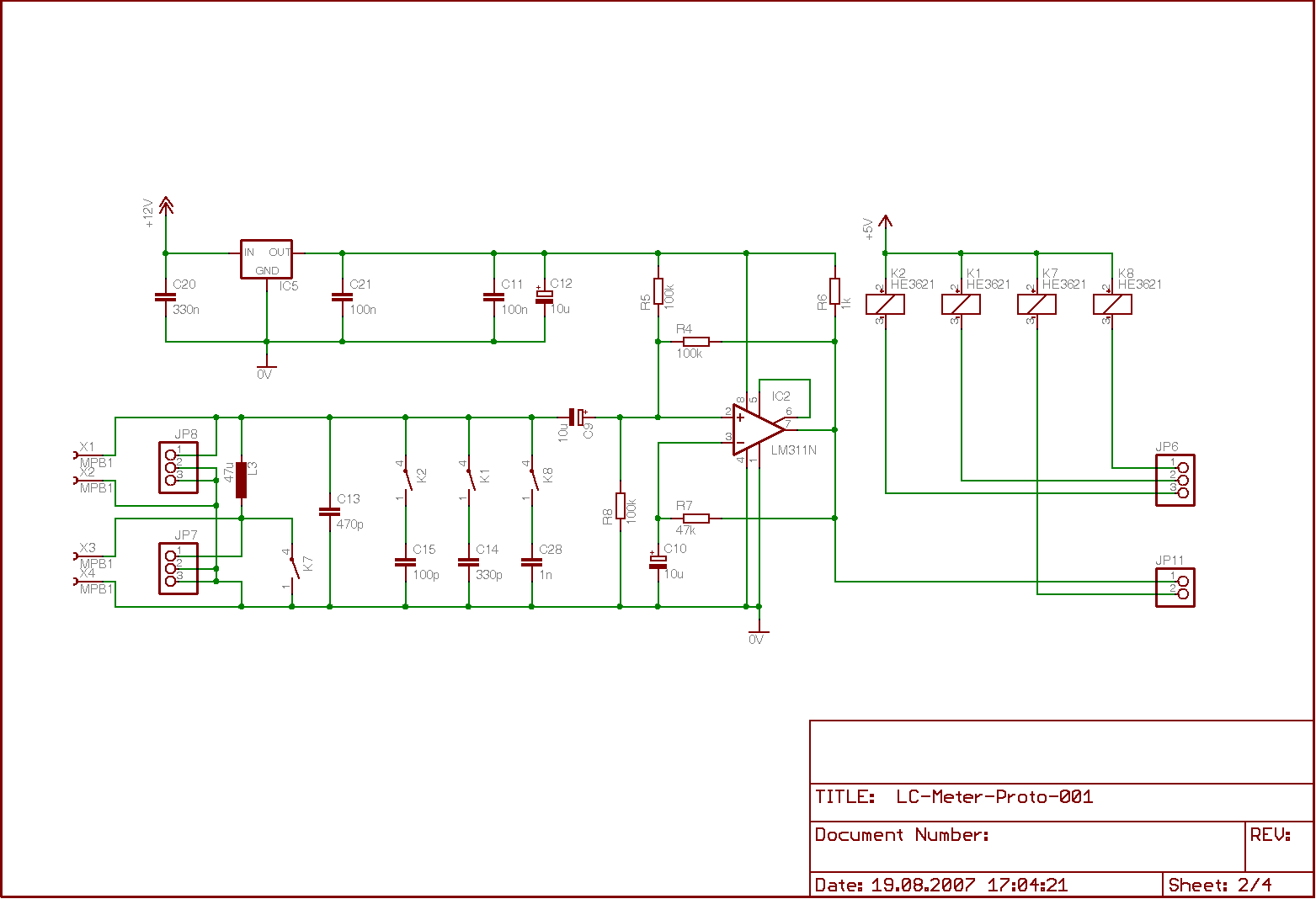
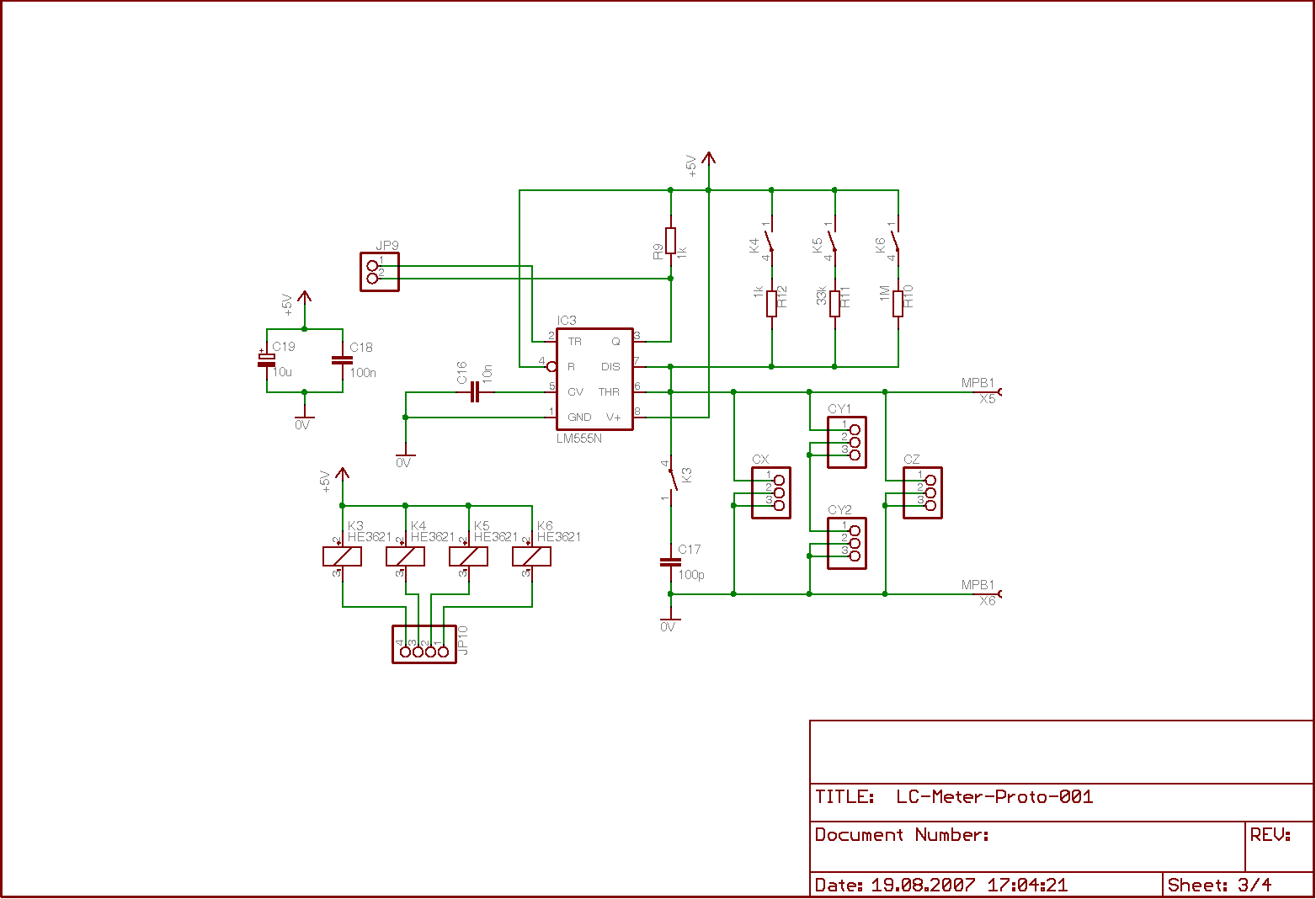
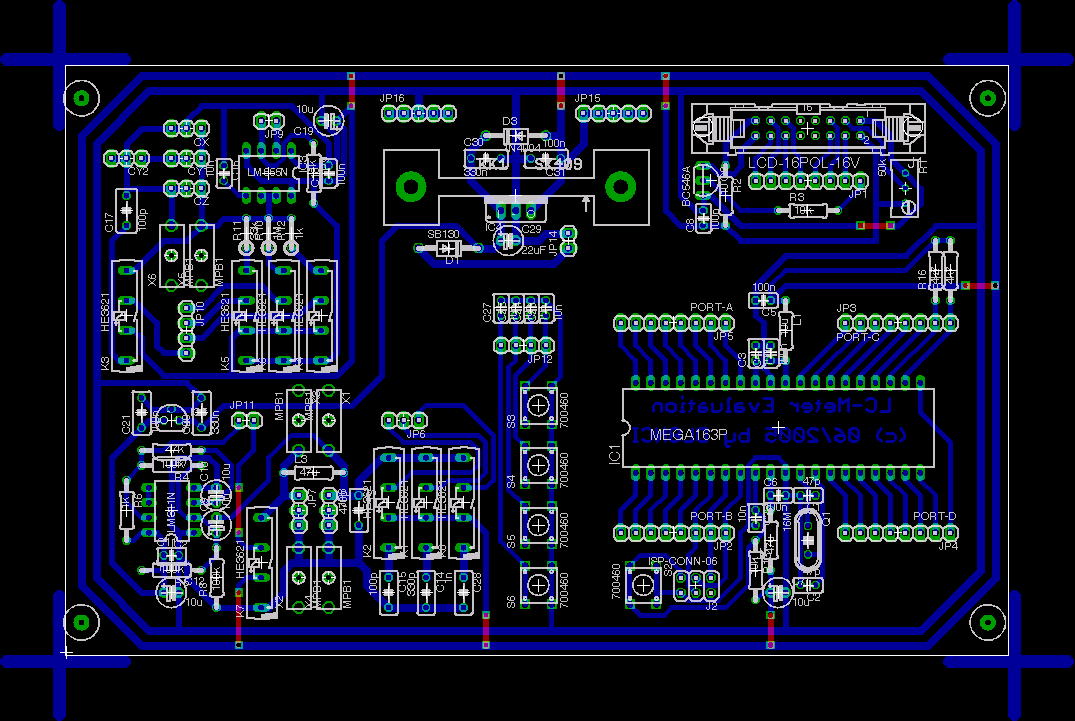
Die folgenden Bilder zeigen den Schaltplan, der auf vier Seiten verteilt ist, sowie das Layout der Platine. Schaltplan und Platine liegen auch als Eagle-Files vor
([3],[4]).

Schaltplan - Teil 1 (Microcontroller)
Schaltplan - Teil 2 (LC-Oszillator)
Schaltplan - Teil 3 (NE555)
Schaltplan - Teil 4 (Stromversorgung)
Layout

4. Induktivitäten

Auf den ersten Blick mag dieses Kapitel überflüssig erscheinen. Was gibt es schon großartiges über Induktivitäten zu bemerken? Eine Induktivität ist durch ihren Wert, angegeben in μH, mH oder gar H doch ausreichend charakterisiert? Daß dem nicht so ist, sieht man allein schon daran, daß eine Induktivität aus Draht aufgebaut ist. Drähte, auch Kupferdrähte, haben einen nicht verschwindenden Widerstand. Beispielsweise hat eine handelsübliche Festinduktivität für 1 mH einen Widerstand von 14 Ω. Widerstände
sind ein Maß für Verluste. Auch das Kernmaterial wird für Verluste sorgen und so für eine weitere Erhöhung der ohmschen Anteile. Weiterhin haben Induktivitäten Anschlußdrähte. Diese, und seien sie auch noch so klein (SMD), haben eine nichtverschwindende Kapazität. Auch abhängig vom Spulenaufbau können weitere kapazitive Anteile hinzukommen. Man könnte das Spiel sogar noch weiter treiben und jedem Paar aus benachbarten Windungen eine Kapazität zuschreiben. Abschließend sei bemerkt, daß vor allem die parasitären Beiträge auch noch frequenzabhängig sein können. Vor allem die Eigenschaften des verwendeten Kernmaterials können eine Ursache dafür sein. Oder auch der Skin-Effekt, der bei zunehmender Frequenz den Strom nur noch in der Nähe der Oberfläche des Drahtes fließen läßt, ist naturgemäß frequenzabhängig.

Wenn man ein Induktivitätsmeßgerät baut, dann muß man sich selbst darüber im klaren sein, welche parasitären Anteile der Spule man bei der Messung neben der primär zu messenden Induktivität darüber hinaus noch berücksichtigen will. Im einfachsten Fall würde man sowohl die ohmschen Verlustwiderstände als auch jegliche Form der Parallelkapazitäten vernachlässigen. Des weiteren würde man alle Größen als frequenzunabhängig annehmen. Eine etwas realistischere Betrachtung wäre, daß man zusätzlich zur
Induktivität die Parallelkapazität versucht zu ermitteln. Dieser Weg soll im weiteren Verlauf auch beschrieben werden.

Übrigens für Kapazitäten kann man analoge Betrachtungen durchführen. Die Zuleitungen liefern einen Beitrag zur Serieninduktivität und die endliche Leitfähigkeit sowie (frequenzabhängige) Verluste im Dielektrikum tragen zu einem Verlustwiderstand bei.

5. Die L-Messung

Wie bereits in der Einführung angedeutet, beruht die Messung einer Induktivität $L$ auf der Messung der Frequenz $f$ bzw der Kreisfrequenz $\omega$ eines Schwingkreises bestehend aus $L$ und $C$ . Die Thomsonschen Schwingungsformel verknüpft diese Größen gemäß:

(4) $\begin{equation*} \omega = 2 \pi f = \frac{1}{\sqrt{L C}} \end{equation*}$

Sind zwei Größen der Gleichung bekannt, so kann die dritte daraus berechnet werden. Für ein Induktivitätsmessgerät wäre ein gängiges Vorgehen, die Frequenz $f$ zu messen und die Kapazität $C$ als bekannt vorauszusetzen. Beispielsweise könnte man einen Kondensator mit genügend genau bekannter Kapazität in den Schwingkreis einbauen. Dann kann $L$ leicht gemäß

(5) $\begin{equation*} L = \frac{1}{(2 \pi f)^2 C} = \frac{1}{\omega^2 C} \end{equation*}$

berechnet werden. In dem hier diskutierten Induktivitätsmeßgerät wird prinzipiell genau so vorgegangen. In der Praxis hat man jedoch mit verschiedenen Schwierigkeiten zu rechnen:

Sehr kleine Induktivitäten bedingen sehr hohe Frequenzen, die sowohl den LM311 als auch den ATMega163 überfordern.
Induktivitäten haben, abhängig vom Wicklungsaufbau, parasitäre Kapazitäten.
Der Aufbau der Schaltung und die Leiterbahnführung sind nicht ohne zusätzliche und unbekannte Kapazitäten realisierbar.
Der im Rückkopplungszweig angeordnete LM311 hat eingangsseitig eine unbekannte, aber nicht verschwindende Kapazität.

Anhand des folgenden Schaltbildes, das ein Auszug aus dem Schaltplan - Teil 2 (LC-Oszillator)
ist, werden die weiteren Einzelheiten diskutiert.

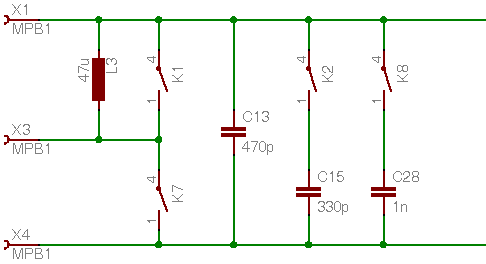
Schaltplan - der Schwingkreis - vereinfacht

Die unbekannte Induktivität $Ö_x$ wird an die Klemmen X3 und X4 angeschlossen. Damit ist sie in Serie zu $L_3$ angeordnet. $C_{13}$ ergänzt die Schaltung zu einem vollständigen Schwingkreis. Hinweis: Der Schalter K1 dient hier zur überbrückung von $L_3$ , während er im Schaltplan noch dazu dient, den 330 pF Kondensator zu schalten. Dieser Kondensator wird jetzt über K2 geschaltet. K8 wird nicht weiter berücksichtigt.

Um die hohen Frequenzen zu vermeiden, die sich aus sehr kleinen zu messenden Induktivitäten ergeben, kann man einerseits die Kreiskapazität erhöhen oder andererseits die Induktivität erhöhen, indem man eine weitere Induktivität $L_3$ zur unbekannten und zu messenden Induktivität $L_x$ in Reihe schaltet: $L = L_3 + L_x$ . Generell gilt als Daumenregel, daß das Verhältnis aus $L$ und $C$ eher groß als klein sein soll. Es ist also ratsamer $L$ zu vergrößern statt $C$ . Wie ein Blick auf den Schaltplan beweist, wurde genau diese zweite Möglichkeit realisiert - genauso wie in der Vorlage ([1]). Ist $L_x = 0$ (oder zumindest sehr viel kleiner als $L_3$ ) so hat der Schwingkreis, der jetzt nur noch aus $L_3$ und $C_{13}$ besteht, eine Eigenfrequenz von rund 1 MHz. Selbst ein sehr kleines $L_s$ kann die Frequenz nur noch erniedrigen.

5.1 Meßvorschrift 1

Zunächst wollen wir $L_3$ nicht berücksichtigen und es mittels K1 kurzschließen, was zur Konsequenz hat, daß $L_x$ nicht wesentlich kleiner als 50 μH sein darf, damit die obere Frequenzgrenze des Oszillators und des ATMega163 nicht überschritten wird. Weiterhin wollen wir annehmen, daß $L_x$ eine parasitäre Parallelkapazität haben kann. Schließlich müssen wir sogar annehmen, daß der Schaltungsaufbau selber einen weiteren unbekannten kapazitiven Beitrag zum gesamten Schwingkreis liefern wird. Diese parasitäre Kapazität von $L_c$ und die Kapazität aus dem Schaltungsaufbau fassen wir unter $C_y$ zusammen. Man sieht sofort, daß zwei Größen zu bestimmen sind: primär $L_x$ und als Dreingabe $C_y$ . Da liegt einem doch sofort der Satz "zwei Gleichungen - zwei Unbekannte" auf der Zunge. Welches sind nun die zwei Gleichungen? Da wir Schwingkreise betrachten, müssen die beiden Gleichungen, die wir benötigen, auf die Thomsonsche Schwingungsformel zurückzuführen sein. Wir können leicht dadurch zwei Gleichungen erzielen, indem wir zwei Messungen durchführen und bei der zweiten Messung ein Bauteil in den Schwingkreis einfügen, dessen Wert wir genau kennen. $C_{13}$ bietet sich sofort an, weil dieser Kondensator über K2 zugeschaltet werden kann.

Messung von	Dabei wirksame Komponenten
$f_1$	$L_x$ , $C_{13}$ , $C_y$
$f_2$	$L_x$ , $C_{13}$ , $C_y$ , $C_{15}$

Die wirksamen Komponenten bei Messung von $f_1$ und $f_2$

(6) $\begin{equation*} L_x = \frac{f_1^2 - f_2^2}{(2 \pi f_1 f_2)^2 C_{15}} \end{equation*}$

(7) $\begin{equation*} C_y = C_{15} \frac{f_2^2}{f_1^2 - f_2^2} - C_{13} \end{equation*}$

Die Herleitung ist hier noch ein wenig detaillierter dargestellt. Die Formeln sind nicht zu komplex und lassen sich leicht auch für einen Microcontroller realisieren. Im folgenden werden ein paar Messergebnisse gezeigt, die die prinzipielle Tauglichkeit dieses Ansatzes belegen.

Messung	nomineller Wert	gemessener Wert	C_y	Bemerkungen
1	2,4 mH	2,41 mH	46,9 pF	Festinduktivität
4	unbekannt	12,1 mH	332 pF	Trafo 230V/15 V auf Sekundärseite gemessen
5	unbekannt	127 μH	34,1 pF	Einlagige Zylinderspule
6	47 μH	47,3 μH	45,4 pF	Festinduktivität
7	unbekannt	4,18 mH	37,1 pF	LW-Spule auf Ferritstab
8	47 μH \|\| 470 pF	47,3 μH	522 pF	Festinduktivität mit Parallelkapazität

Einige Beispielmessungen zur Messvorschrift 1

Die Nummern, zu denen es keine Messungen gibt, konnten hier noch nicht durchgeführt werden, weil die Induktivitäten mit wenigen 10 μH zu gering waren. Der Oszillator ist garnicht erst angeschwungen. Was man erkennt, ist, daß die Werte der bekannten Induktivitäten sich gut reproduzieren lassen. Die Kapazität der gesamten Meßanodnung dürfte bei rund 30 pF liegen, wie die Messung der einlagigen Zylinderspule, die von hause aus kapazitätsarm ist, belegt. Eine Zusatzkapazität von 470 pF wird auch ziemlich korrekt
ermittelt (Messungen 6 und 8). Die Langwellenspule ist ebenfalls recht kapazitätsarm, während der Trafo eine schon recht hohe Kapazität aufweist.

Als Schmankerl sei noch folgendes erwähnt: Selektiert man aus einer größeren Menge von Festinduktivitäten zwei Stück, deren gemessene Induktivitäten $L_x$ und gemessene Kapazitäten $C_y$ möglichst gleich sind, so kann man beide Induktivitäten dann in Reihe schalten und erneut messen. Die gemessene Induktivität wird sich dann verdoppeln während der gemessene Wert von $C_y$ sinken wird, weil die parasitären Kapazitäten der beiden Induktivitäten jetz in Reihe geschaltet sind und sie sich somit halbieren. Das doppelte der Differenz der beiden $C_y$ -Werte ist die parasitäre Kapazität einer Induktivität. Der Versuch, dies mit der 47 μH-Festinduktivität durchzuführen ergab eine parasitäre Kapazität von etwa 15 pF. Das heißt, in Messung 6 gehen 15 von den 45,4 pF auf das Konto der Induktivität und rund 30 pF stammen vom Schaltungsaufbau. Auch das ist im Einklang mit den Ergebnissen der kapazitätsarmen Spulen.

5.2 Meßvorschrift 2

Jetzt möchten wir auch kleine Induktivitäten messen und dazu ist es notwendig $L_3$ der unbekannten Induktivität $L_x$ in Reihe zu schalten. Daraus ergibt sich die einfachste Meßvorschrift: Der Schwingkreis besteht nur aus $L_x$ , $L_3$ und $C_{13}$ . Die Bauteile werden als ideal betrachtet, die Bauteilewerte von $L_3$ und $C_{13}$ werden als exakt angenommen, die Einflüsse der Leiterbahnen werden vernachlässigt und der Einfluß des LM311 auf die Schwingfrequenz wird ebenfalls vernachlässigt. $C_y$ ist also null. Dann läßt sich $L_x$ aus der gemessenen Frequenz $f_1$ , deren Meßfehler ebenfalls vernachlässigt werden kann, wie folgt berechnen:

Messung von	Dabei wirksame Komponenten
$f_1$	$L_x$ , $L_3$ , $C_{13}$

Die wirksamen Komponenten bei Messung von $f_1$

(8) $\begin{equation*} L_x = \frac{1}{(2 \pi f_1)^2 C_{13}} - L_3 \end{equation*}$

Ein Anfang ist gemacht. Aber diese Lösung ernsthaft weiter zu vefolgen, lohnt nicht. Unter realen Bedingungen werden zumindest die Werte der verwendeten Bauteile $C_{13}$ und $L_3$ eine nichtverschwindende Toleranz aufweisen. Leicht (für den Bastler) beschaffbare Kondensatoren lassen sich bis auf weinige Prozent genau fertigen; bei Induktivitäten liegen die Toleranzen kaum unter 10%. Ganz grob kann man daraus schließen, daß gemessene Induktivitäten von 5 μH oder weniger einen Fehler von mindestens 100% aufweisen werden. Die Messung ist dann praktisch wertlos. Je kleiner also $L_x$ ist, desto größer ist der Einfluß des Fehlers von $L_3$ auf den Meßwert. Der Fehler von $C_{13}$ spielt dann nur noch eine untergeordnete Rolle. Umgekehrt - je größer $L_x$ ist desto geringer ist der Einfluß von $L_3$ auf das Meßergebnis. Dann dominiert nur noch der Fehler von $C_{13}$ . Da $C_y$ hier nicht berücksichtigt wird, wollen wir uns mit dieser Meßvorschrift nicht weiter befassen und uns gleich der nächste Meßvorschrift zuwenden, die zeigt, wie man zunächst den Fehler von $L_3$ eliminieren kann.

5.3 Meßvorschrift 3

Diese Meßvorschrift eliminiert die Toleranz der Induktivität $L_3$ , indem zwei Messungen durchgeführt werden wobei im einen Fall $L_x$ am Schwingkreis beteiligt ist während im anderen Fall $L_x$ kurzgeschlossen ist und damit 0 ist. Der Schalter K7 dient dazu, die unbekannte Induktivität $L_x$ zu überbrücken. Die erste Messung wird also gemäß der Meßvorschrift 2 durchgeführt wobei K7 offen ist. Sie lefert die Frequenz $f_1$ die zum Schwingkreis bestehend aus $L_x$ , $L_3$ und $C_{13}$ gehört. Die zweite Messung liefert die Frequenz $f_2$ , die zu einem Schwingkreis gehört, der nur aus $L_3$ und $C_{13}$ besteht. Daraus kann $L_3$ leicht berechnet werden. Dieser Schwingkreis hat natürlich eine höhere Resonanzfrequenz als derjenige, der bei der Messung von $f_1$ benutzt wurde. Also $f_2 > f_1$ .

Messung von	Dabei wirksame Komponenten
$f_1$	$L_x$ , $L_3$ , $C_{13}$
$f_2$	$L_3$ , $C_{13}$

Die wirksamen Komponenten bei Messung von $f_1$ und $f_2$

(9) $\begin{equation*} L_3 = \frac{1}{(2 \pi f_2)^2 C_{13}} \end{equation*}$

(10) $\begin{eqnarray*} L_x & = & \frac{1}{(2 \pi f_1)^2 C_{13}} - L_3 \\ & = & \frac{1}{(2 \pi f_1)^2 C_{13}} - \frac{1}{(2 \pi f_2)^2 C_{13}} \\ & = & \frac{1}{4 \pi^2 C_{13}} \left( \frac{1}{f_1^2} - \frac{1}{f_2^2} \right) \\ & = & \frac{f_2^2 - f_1^2}{(2 \pi f_1 f_2)^2 C_{13}} \end{eqnarray*}$

Der Wert von $L_3$ tritt, nachdem $L_3$ in die untere Gleichung eingestzt wurde, nicht mehr auf und kann somit auch keinen Beitrag mehr zum Fehler leisten. Bleibt immer noch $C_y$ , das für kleine Induktivitäten nicht berücksichtigt wurde. Die folgende Meßvorschrift 4a und alternativ 4b zeigen einen Weg, auch eine Aussage über $C_y$ zu erhalten.

5.4 Meßvorschrift 4a

Jetzt wird zusätzlich noch eine dritte Messung durchgeführt. $f_1$ und $f_2$ bestimmen sich wie oben. $f_3$ wird gemessen während $L_x$ kurzgeschlossen ist, und $C_{15}$ über K2 zugeschaltet ist. Insgesamt liegen damit drei Gleichungen vor mit den drei Unbekannten $L_x$ , $L_3$ und $C_y$ . Es gäbe sogar noch eine vierte Möglichkeit zu messen: nämlich bei offenem K7 und geschlossenem K2. Dies würde jedoch zu einem überbestimmten Gleichungssystem führen, das normalerweise nicht lösbar ist, sondern nur im Sinne eines geringsten Fehlers - nicht unmöglich, aber ich habe das nicht weiter betrachtet. Was aber leicht geht, ist diese vierte Messung trotzdem durchzuführen und die Ergebnisse dann für $L_x$ zu vergleichen. Abweichungen deuten dann auf Besonderheiten der unbekannten Induktivität $L_x$ hin. Siehe auch 5.5.

Messung von	Dabei wirksame Komponenten
$f_1$	$L_x$ , $L_3$ , $C_{13}$ , $C_y$
$f_2$	$L_3$ , $C_{13}$ , $C_y$
$f_3$	$L_3$ , $C_{13}$ , $C_y$ , $C_{15}$

Die wirksamen Komponenten bei Messung von $f_1$ , $f_2$ und $f_3$

(11) $\begin{equation*} L_3 = \frac{f_2^2 - f_3^2}{(2 \pi f_2 f_3)^2 C_{15}} \end{equation*}$

(12) $\begin{equation*} C_y = C_{15 }\frac{f_3^2}{f_2^2 - f_3^2} - C_{13} \end{equation*}$

(13) $\begin{equation*} L_x = \frac{(f_2^2 - f_1^2)(f_2^2 - f_3^2)}{(2 \pi f_1 f_2 f_3)^2 C_{15}} \end{equation*}$

Interessant ist natürlich die dritte Gleichung, die die drei gemessenen Frequenzen $f_1$ , $f_2$ und $f_3$ sowie die Kapazität $C_{15}$ mit der Induktivität $L_x$ in Beziehung setzt. Die anderen beiden Gleichungen wurden nur der Vollständigkeit halber angegeben. In Einzelfall mag es durchaus interessant sein, $C_y$ zu bestimmen, denn dieser Wert sagt ja etwas über die parasitären Kapazitäten des Aufbaus aus. Für $C_{13}$ ist tatsächlich der aufgedruckte Wert einzusetzten. Die Toleranz wurde ja $C_y$ zugeschlagen. Auch $L_3$ läßt sich aus den drei gemessenen Frequenzen und $C_{15}$ ermitteln. Da jetzt alle Werte nur noch von den Frequenzen und $C_{15}$ abhängen, kann man folgern, daß man sich diesen Kondensator mit der niedrigsten Toleranz und möglichst auch mit einer hohen Langzeitstabilität beschaffen soll. Außerdem soll seine Einbindung in das gesamte Layout so wenig wie möglich weitere parasitäre Kapazitäten beisteuern. Hier gilt es alle Leiterbahnen so kurz wie möglich auszuführen. Bei einem Kondensator mit 330pF und einer Toleranz von 2,5% bedeuten 8pF Aufbau- und Leiterbahnkapazitäten einen erheblichen Verlust an Genauigkeit. Andererseits hoffe ich, daß es mir gelungen ist, deutlich unter den 8 pF zu liegen.

Die mit dem Prototypen durchgeführten Messungen gemäß Vorschrift 4a ergaben folgende Ergebnisse:

Messung	nomineller Wert	gemessener Wert	L₃	C_y	Bemerkungen
1	2,4 mH	2,41 mH	46,2 μH	43,4 pF	Festinduktivität
2	15 μH	14,8 μH	46,2 μH	43,3 pF	Festinduktivität
3	10 μH	9,2 μH	46,2 μH	43,4 pF	Festinduktivität
4	unbekannt	18,8 mH	46,2 μH	43,5 pF	Trafo 230V/15 V auf Sekundärseite gemessen
5	unbekannt	122 μH	46,2 μH	43,5 pF	Einlagige Zylinderspule
6	47 μH	45,4 μH	46,2 μH	43,5 pF	Festinduktivität
7	unbekannt	4,04 mH	46,2 μH	43,6 pF	LW-Spule auf Ferritstab
8	47 μH \|\| 470 pF	72,8 μH	46,2 μH	43,8 pF	Festinduktivität mit Parallelkapazität
9	Kurzschluß (L=0)	-0,02 μH	46,1 μH	43,2 pF	2 cm Leiterschleife
10	10 μH \|\| 470 pF	10,8 μH	46,2 μH	44,1 pF	Festinduktivität mit Parallelkapazität

Einige weitere Beispielmessungen

Bei allen Messungen fällt auf, daß die Werte von $L_3$ und $C_y$ kaum variieren. Auf den ersten Blick ein gutes Zeichen. Aber der Vergleich mit den Messungen aus 5.1 liefert Widersprüche. Die Induktivitäten der Bauteile mit hoher Parallelkapazität (Messung 4 und 8) liefern einen zu hohen Wert für $L_x$ und zu kleine Werte für $C_y$ . Betrachtet man insbesondere die Messung 8, So fällt auf, daß die Parallelkapazität zu $L_x$ sich ausschließlich auf den Wert der Induktivität von $L_x$ auswirkt und nicht, wie erwartet, als Erhöhung des Wertes von $C_y$ . Schaltet man jedoch die 470 pF parallel zu $C_{13}$ , so wird für $C_y$ ein Wert von 522 pF ermittelt, was ein durchaus vernünftiger Wert ist. Diese Messung zeigt, daß die gewählte Konfiguration nicht dazu geeignet ist, Parallelkapazitäten zu $L_x$ richtig zu ermitteln. Diese Konfiguration liefert also nur dann vernünftige Resultate, wenn $L_x$ eine ideale (oder doch zumindest kapazitätsarme) Induktivität ist. Letzten Endes ist das aber nicht verwunderlich, denn der Schwingkreis hat hier ein viel komplizierteren Aufbau. $L_x$ bildet mit seiner parasitären Kapazität, die nur ein Teil von $C_y$ ist, bereits einen Schwingkreis, dem in Reihe die Induktivität $L_3$ geschaltet ist. Dieser Anordnung sind dann noch die Kapazitäten $C_{13}$ , $C_{15}$ , und die schaltungsbedingten Anteile von $C_y$ parallelgeschaltet.

Messung 9 liefert einen negativen Wert. Das kann immer mal wieder passieren, wenn sehr große, fast gleiche Zahlen voneinander subtrahiert werden. Möglicherweise führt das Schließen von K7 zu einer Erhöhung parasitärer Kapazitäten, die die Reduzierung der Induktivität $L_x$ überkompensiert.

5.5 Meßvorschrift 4b

Wie bereits bei der Meßvorschrift 4a (5.4) angedeutet, gibt es noch eine weitere, die sich in der Ausführung der dritten Messung unterscheidet. Alternativ wird ausgehend von der ersten Messung, bei der $L_x$ nicht kurzgeschlossen ist, $C_{15}$ zugeschaltet und dabei $f_4$ gemessen. Es sind also alle Bauteile am Schwingkreis beteiligt, während in der Meßvorschrift 4a die unbekannte Induktivität $L_x$ ja kurzgeschlossen und somit nicht wirksam war. Das Ergebnis ist der folgende Satz von Gleichungen:

Messung von	Dabei wirksame Komponenten
$f_1$	$L_x$ , $L_3$ , $C_{13}$ , $C_y$
$f_2$	$L_3$ , $C_{13}$ , $C_y$
$f_4$	$L_x$ , $L_3$ , $C_{13}$ , $C_y$ , $C_{15}$

Die wirksamen Komponenten bei Messung von $f_1$ , $f_2$ und $f_4$

(14) $\begin{equation*} L_3 = \frac{f_1^2 - f_4^2}{(2 \pi f_2 f_4)^2 C_{15}} \end{equation*}$

(15) $\begin{equation*} C_y = C_{15} \frac{f_4^2}{f_1^2 - f_4^2} - C_{13} \end{equation*}$

(16) $\begin{equation*} L_x = \frac{(f_2^2 - f_1^2)(f_1^2 - f_4^2)}{(2 \pi f_1 f_2 f_4)^2 C_{15}} \end{equation*}$

Es fällt auf, daß die Gleichungen strukturell sehr ähnlich aussehen. Natürlich müssen die beiden Meßvorschriften 4a und 4b zum selben Ergebnis für alle drei Größen $L_3$ , $C_y$ und $L_x$ führen. In der Realität werden sie das jedoch nicht tun. Wir werden zufrieden sein, wenn die drei Größen nicht zu sehr voneinander abweichen. Vor allem $L_x$ sollte zwischen beiden Varianten weniger variieren, als es der Meßfehler vermuten läßt. Wenn $L_x$ keine parasitären Kapazitäten hat, dann werden die Ergebnisse konsistent sein. Hat $L_x$ aber z.B. sogar einen Kondensator parallel geschaltet, dann werden die Messungen massiv abweichen. Das kann beispielsweise auch dann passieren, wenn die zu messende Spule gar keinen Kondensator eingebaut hat. Entweder sie hat dann einen Wicklungsaufbau, der zu einer hohen Kapazität führt, oder es handelt sich um einen Transformator mit großem übersetzungsverhältnis. Mißt man auf der Seite mit der geringen Windungszahl (Primärseite, $n_1$ Windungen), dann werden die Wicklungskapazitäten (oder sogar eine echte angeschlossene Kapazität) der Spule mit der hohen Windungszahl (Sekundärseite, $n_2$ Windungen) so transformiert daß sie um den Faktor $ü^2$ an der Primärspule erscheinen. $ü$ ist das Windungsverhältnis der Sekundärspule und der Primärspule.

Das Problem mit den Kapazitäten der zu messenden Induktivität ist, daß sie nicht parallel zum gesamten Schwingkreis bestehend aus $L_x$ und $L_3$ liegen, sondern nur parallel zu $L_x$ , was ja seinerseits nur ein Teil der gesamten Induktivität des Schwingkreises ist. Das gesamte Gebilde ist dann jedenfalls kein einfacher Schwingkreis mehr.

Die Messungen nach der Meßvorschrift 4a haben ja schon gezeigt, daß die Ergebnisse mir Vorsicht zu genießen sind. Trotzdem wurden die Messungen mit den selben Bauteilen in der Variante 4b wiederholt. Nachfolgend die Ergebnisse.

Messung	nomineller Wert	gemessener Wert	L₃	C_y	Bemerkungen
1	2,4 mH	2,40 mH	46,1 μH	46,4 pF	Festinduktivität
2	15 μH	14,9 μH	47,1 μH	34,5 pF	Festinduktivität
3	10 μH	9,2 μH	46,9 μH	36,4 pF	Festinduktivität
4	unbekannt	12,1 mH	29,7 μH	331 pF	Trafo 230V/15 V auf Sekundärseite gemessen
5	unbekannt	126 μH	47,5 μH	29,7 pF	Einlagige Zylinderspule
6	47 μH	46,5 μH	47,3 μH	32,0 pF	Festinduktivität
7	unbekannt	4,14 mH	46,9 μH	36,9 pF	LW-Spule auf Ferritstab
8	47 μH \|\| 470 pF	55,6 μH	35,3 μH	202 pF	Festinduktivität mit Parallelkapazität
9	Kurzschluß (L=0)	-0,02 μH	46,2 μH	42,4 pF	2 cm Leiterschleife
10	10 μH \|\| 470 pF	10,6 μH	45,4 μH	54,0 pF	Festinduktivität mit Parallelkapazität

Einige weitere Beispielmessungen

Im Vergleich zu den Messungen in 5.4 fällt hier auf, daß $L_3$ und vor allem $C_y$ stärker variieren. Das ist ein Indiz dafür, daß parasitäre Kapazitäten von $L_x$ vorhanden sind und sie sich unterschiedlich stark auf $L_3$ und $C_y$ auswirken. Messung 8 mit der absichtlich zugefügten Kapazität und Messung 4 mit dem Transformator zeigen dies deutlich. Die gemessene Induktivität fällt kleiner aus, während ein Teil der Parallelkapazität jetzt bei $C_y$ zu finden ist. Schaltet man bei Messung 8 jedoch die 470 pF wieder parallel zu $C_{13}$ , so wird für $C_y$ ein Wert von 511 pF ermittelt, was auch hier ein durchaus vernünftiger Wert ist. Die Messung 4 mit dem Trafo zeigt noch etwas anderes: Sowohl $L_x$ als auch $C_y$ stimmen sehr gut mit den Werten aus 5.1 überein. Das liegt daran, daß $L_3$ sehr klein verglichen mit $L_x$ ist.

Zum negativen Wert der Messung 9 gilt ebenfalls das in 5.4 gesagte.

Tendenziell scheint diese Meßvorschrift die etwas besseren Ergebnisse zu liefern. Die Werte von $L_3$ liegen näher an den nominellen Werten dran. Aber auch hier muß als Fazit festgehalten werden, daß die gewählte Konfiguration zur Messung von Kapazitäten parallel zu $L_x$ nicht geeignet ist, vor allem wenn $L_x$ von der selben Größenordnung wie $L_3$ ist. Ist jedoch $L_x < L_3$ so wirkt sich eine parasitäre Kapazität kaum noch auf das Ergebnis von $L_x$ aus, wie die Messungen 10 im Vergleich zu 3 zeigen. $C_y$ bleibt aber trotzdem wertlos.

6. Die C-Messung

Kapazitäten können wir auf zwei Wegen messen. Einmal können wir wieder auf einen Schwingkreis zurückgreifen, bei dem wir den Wert der Induktivität kennen und aus der gemessenen Frequenz auf die Kapazität rückschließen können. Die bereits mehrfach zitierte Thomsonsche Schwingungsformel wird dazu einfach nach C aufgelöst und man erhält:

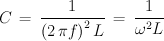
Alternativ wird zur Messung der Kapazität der gute alte Timer NE555 (z.B. [6]) verwendet, der von vielen Herstellern angeboten wird. Er kennt zwei Betriebsarten, wobei in diesem Einsatzfall er als sogenannter monostabiler Multivibrator, auch bekannt als Monoflop, betrieben wird. Grundidee ist, daß die Ladezeit (oder auch Entladezeit) eines Kondensators in einem formelmäßigen Zusammenhang mit seiner Kapazität steht.

6.1 Die C-Messung basierend auf einem Schwingkreis

Da wir auch hier wieder sehr kleine Kapazitäten C_x messen wollen, folgen wir der selben Strategie wie bei der Messung kleiner Induktivitäten L_x. Ähnlich, wie dort die Serienschaltung aus L_x und L₃ sicherstellt, daß die Induktivität im Schwingkreis einen Minimalwert, nämlich den von L₃, nicht unterschreitet, wird hier durch Parallelschaltung von C_x und C₁₃ erreicht, daß die Kapazität nicht unter den Wert von C₁₃ fällt. Die Schwingfrequenz im Schwingkreis wird daher nicht über rund 1 MHz liegen. Im folgenden als Wiederholung nochmal der relevante Ausschnitt aus dem Schaltplan.

Wir hatten bei der L-Messung immer die parasitären Kapazitäten der Induktivität und des Schaltungsaufbaus durch C_y ausgedrückt und versucht, diesen Wert zu bestimmen. Da wir uns bei der C-Messung nicht weiter dafür interessieren, schlagen wir sie einfach dem Kondensator C₁₃ zu.

Die Größen C_x, L₃ und C₁₃ sind als unbekannt zu betrachten. Es müssen also minimal drei Frequenzmessungen durchgeführt werden, bei denen der Schwingkreis so zu konfigurieren ist, daß drei Gleichungen dabei entstehen. Die folgende Aufstellung zeigt eine Möglichkeit:

Messung von	Dabei wirksame Komponenten
f₁	C₁₃, L₃
f₂	C₁₃, C₁₅, L₃
f₃	C_x, C₁₃, L₃

Die wirksamen Komponenten bei Messung von f₁, f₂ und f₃

Damit ist C₁₅ derjenige Kondensator, dessen Genauigkeit direkt in das Meßergebnis einfließt. Sein Wert muß daher so genau wie möglich bekannt sein. Die folgenden Formeln geben an, wie aus den gemessenen Frequenzen neben L₃ und C₁₃ vor allem die zu bstimmende Kapazität C_x zu berechnen ist.

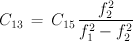
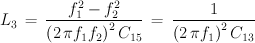
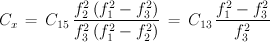
Alternativ besteht auch hier wieder die Möglichkeit - wie bei der Messung der Induktivitäten - die dritte Frequenzmessung mit zugeschaltetem Kondensator C₁₅ durchzuführen. Die Frequenz in dieser Konfiguration bezeichnen wir hier mit f₄.

Messung von	Dabei wirksame Komponenten
f₁	C₁₃, L₃
f₂	C₁₃, C₁₅, L₃
f₄	C_x, C₁₃, C₁₅, L₃

Die wirksamen Komponenten bei Messung von f₁, f₂ und f₃

Die Werte von C₁₃ und L₃ berechnen sich genau so wie vorher; nur die Berechnung von C_x erfolgt deutlich anders.

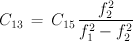
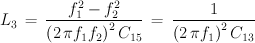
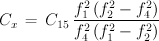
Elegant wäre es, den Kondensator C_x über ein Relais unter der Kontrolle des Microcontrollers zuzuschalten. Das wurde aber nicht vorgesehen, so daß die Bedienung des LC-Meters in diesem Meßmodus ein wenig anders erfolgt. Man muß manuell festlegen, ob man gerade die f₁ und f₂-Messung ohne C_x durchführt, oder die eigentliche f₃ bzw. f₄-Messung mit C_x.

Die parasitären Kapazitäten einer Induktivität liegen in einer Größenordnung, die das LC-Meter leicht bestimmen kann und deren Nichtberücksichtigung das Meßergebnis deutlich beeinträchtigen kann. Das Gegenstück bei der Kapazitäsmessung wären demnach parasitäre Induktivitäten, die unter anderem von den Zuleitungen kommen können. Wir werden solche Induktivitäten, die zumeist unter 1 μH liegen;, nicht weiter berücksichtigen.

6.2 Die C-Messung basierend auf der Messung der Ladezeit (NE555)

Der NE555 (auch als LM555 bekannt) [6] ist ein immer wieder gern genommener Baustein, wenn es darum geht, mittels eines Widerstandes und eines Kondensators eine Impulslänge festzulegen. Genau so wird der Baustein auch hier verwendets wobei er in der monostable operation betrieben wird (monostabiler Multivibrator, Monoflop). Das folgende Bild zeigt den wesentlichen Schaltungsauszug so weit er zum Verständnis relevant ist.

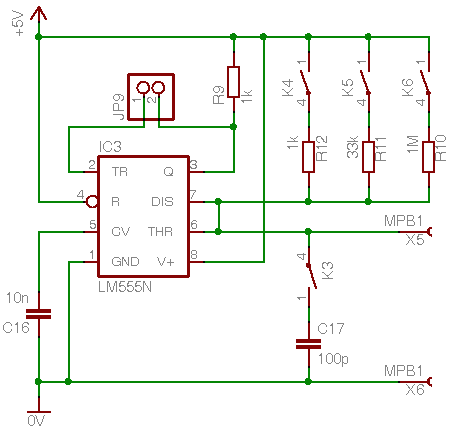
Ein Übergang von High nach Low am Triggereingang TR (Pin 2) bewirkt, daß der Ausgang Q (Pin 3) auf High wechselt. Abhängig von der Dimensierung der zeitbestimmenden Bauteile bleibt der Ausgang für die Zeit Δt auf High bevor er wieder auf Low wechselt. Der Triggerimpuls sollte dabei deutlich kürzer als Δt sein. Die Bauteile, die die Zeit Δt bestimmen, sind

der unbekannte Kondensator C_x, der an die Anschlüsse X5 und X6 angeschlossen wird,
der Kondensator C₁₇, der über K3 zugeschaltet werden kann und dann parallel zu C_x liegt,
einer der drei Widerstände R₁₀, R₁₁, R₁₂.

Ganz allgemein berechnet sich die Impulsdauer Δt gemäß folgender Formel:

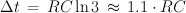
Das heißt, die Kapazität C ist direkt proportional zur gemessenen Zeit Δt und hängt sonst nur noch vom Wert des Widerstandes R ab. Somit kann die Kapazitätsmessung auf eine Widerstandsmessung (und natürlich eine Zeitmessung) zurückgeführt werden. Der Faktor ln3, dessen Wert ungefähr 1,1 ist, rührt daher, daß der Kondensator C bis auf 2/3 der Betriebsspannung aufgeladen wird. Löst man nach C auf, so erhält man:

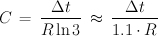
Die Kapazität C setzt sich - nicht unerwartet - aus mehreren Teilkapazitäten zusammen: Zunächst natürlich aus der unbekannte Kapazität C_x, die zu messen ist, dann aus der parasitäre Kapazitäten C_y die vor allem vom Layout und der Verkabelung herrühren und optional aus der Kapazität C₁₇.

Der Faktor ln3, dessen Wert ungefähr 1,1 ist, rührt daher, daß der Kondensator C bis auf 2/3 der Betriebsspannung aufgeladen wird.

6.3 Ein paar Beispiele

Im folgenden werden ein paar Beispiele vorgestellt, die wiederum die Tauglichkeit der Messungen belegen sollen

Messung	nomineller Wert	LC-Kreis (a)	LC-Kreis (b)	NE555	R (NE555)	Bemerkungen
1	470 pF	481 pF	482 pF	480 pF	1 MΩ	FKC?
2	470 pF + 10 μH	527 pF	515 pF	481 pF	1 MΩ	Serienschaltung
3	8,2 pF	8,3 pF	8,4 pF	8,2 pF	1 MΩ	Keramikkondensator
4	100 nF	92,4 nF	92,4 nF	98,8 nF	33 kΩ	Vielschichtkondensator
5	100 nF	98,3 nF	98,3 nF	97,0 nF	33 kΩ	MKS
6	330 nF	374 nF	374 nF	359 nF	33 kΩ	MKS
7	100 pF	95,0 pF	95,3 pF	95,5 pF	1 MΩ	FKC?

Einige Beispielmessungen

Die höchste messbare Kapazität liegt bei ungefähr 330 nF. 470 nF führen bereits zu unsinnigen Resultaten. Beide Varianten liefern praktisch identische Messwerte. Eine zugeschaltete Induktivität führt zu einer Erhöhung der Kapazität; in der zweiten Variante fällt sie aber nicht so groß aus, wie in der ersten. Die Messung mittels NE555 zeigt keine Abhängigkeit von einer vorhandenen Serieninduktivität.

7. Messung des Kopplungsfaktors

Endlich ist es so weit. Wir sind am Ziel. Wobei zugegebenermaßen das Kapitel über die Kapazitätsmessung keinen weiteren Beitrag zur urspürunglichen Frage - nämlich wie groß ist der Kopplungsfaktor zweier Wicklungen auf einem gemeinsamen Kern - geleistet hat. Gemessen wurden

Eine Mittelwellenspule (bezeichnet mit L) aus dem Kosmo Experimentierkasten Elektroniklabor XG (Siebziger Jahre) ohne Kern.
wie zuvor, jedoch mit Kern
Ein Wicklungspaar für Mittelwellenempfang auf einem Ferritstab
Ein Wicklungspaar für Langwellenempfang auf einem Ferritstab
Zum Zeitpunkt der Aufbereitung dieses Artikels liegt mir leider kein Ringkern, wie eingangs genannt mehr vor. Daher kann ich dazu keine Ergebnisse mehr vorstellen.

Spulen, zu denen der Kopplungsfaktor bestimmt worden ist

Das Bild zeigt die Teile im Detail. Oben die Spule aus dem Experimentierkasten, darunter der Ferritstab auf dessen linker Seite die Langwellenspulen und auf dessen rechter Seite die Mittelwellenspulen angeordnet sind. Gemessen wurden jeweils die Induktivitäten der einzelnen Wicklungen L₁ und L₂ sowie die Induktivitäten der Serienschaltung L_x und der Antiserienschaltung L_y. Berechnet wurde dann gemäß

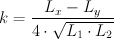
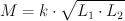
der Kopplungsfaktor k und die Gegeninduktivität M. Die folgende Tabelle führt die Ergebnisse aus.

Messung	L₁	L₂	L_x	L_y	k	M	Bemerkungen
1	149 μH	13,5 μH	193 μH	130 μH	0,35	15,8 μH	ohne Kern
2	229 μH	22,8 μH	332 μH	174 μH	0,55	39,5 μH	mit Kern
3	254 μH	28,1 μH	394 μH	171 μH	0,66	55,8 μH	MW-Spulen auf Ferritstab
4	4071 μH	56,2 μH	4965 μH	3437 μH	0,88	382 μH	LW-Spulen auf Ferritstab

Einige Beispielmessungen

Den Ergebnissen kann man folgende einfache Erkenntnisse entnehmen:

Ein Kern erhöht den Kopplungsfaktor (Messung 1 und 2)
Mittelwellenspulen sind im Grunde doch recht ähnlich aufgebaut (Messung 2 und 3)
Liegen die Wicklungen übereinander, so ist der Kopplungsfaktor größer, als wenn sie nebeneinanderliegen (Messung 3 und 4)

8. Auszüge aus dem Quellcode

Nachdem die bisherigen Kapitel einige theoretische und grundsätzuliche Aspekte der Meßtechnik beleuchtet haben, soll jetzt der Schwerpunkt auf den Quellcode gelenkt werden. Der Prototyp wurde in C implementiert und findet leicht im Flash-Speicher des Atmel ATmega163 Platz. Dieser Typ ist heute veraltet; eine Implementierung in einem aktuellen ATmega16x sollte - bis auf eventuell leicht abweichende Register- oder Interruptnamen - kein Problem darstellen. Als Entwicklungsumgebung wurde das AVRStudio 4.15 [8] zusammen mit dem GNU-C-Compiler 4.2.2 aus WinAVR-Suite [9] und der avr-libc in der Version 1.6.0 [10]] benutzt. Die Programmierung erfolgte über das Starter-Kit STK500 [11] im SPI-Mode. Der gesamte Quellcode ist unter [3] nachzulesen. Im folgenden werden einige wichtige Teilaspekte behandelt.

8.1 Frequenzmessung

Alle hier vorgestellten Kapazitäts- und Induktivitätsmessungen, denen ein Schwingkreis zugrunde liegt, basieren auf der Messung von Frequenzen. Damit ist dies die Hauptaufgabe, die der ATmega163 zu erfüllen hat. Frequenzmessungen können grundsätzlich auf zwei Arten erfolgen: Messung der Periodendauer einer Schwingung und Zählen der Schwingungen während eines vorgegebenen Zeitintervalls. Hier wird der zweite Ansatz verfolgt, weil Periodendauermessungen nur im Bereich unter einigen kHz sinnvoll sind, während hier bei den L- und C-Messungen Frequenzen ab ca. 10 kHz bis zu rund 1 MHz zu erwarten sind.

Wir benötigen also zwei Timer/Counter. Einer (Timer/Counter 2) wird als Timer konfiguriert während der andere (Timer/Counter 1) als Zähler (Counter) verwendet wird.

#include <avr/interrupt.h>

volatile uint32_t CNT;			// the global counter
volatile uint8_t ready;			// 0:counting; 1:ready
uint8_t n_CNT;				// number of measurements executed
double t_gate;				// the gate-time
#define TF 200				// ca. 50 ms

// the timer2-compare interrupt
ISR(TIMER2_COMP_vect) {
	uint16_t l,h;

	TCCR1B = 0;			// stop counter
	TCCR2 = 0;			// stop timer

	l = TCNT1L;			// read counter and ...
	h = TCNT1H;
	CNT = CNT + l + (h << 8);	// ... add to global counter

	ready=1;			// notify main program
	}

// measure one time the current frequency
void Measure_1(void) {

	cli();				// disable interrupts

	TCCR1A = 0x00;			// setup timer/counter 1 as counter
	TCCR1B = 0x00;

	TCNT1H = 0;			// clear timer/counter registers
	TCNT1L = 0;

	TCCR2 = 0x00;			// setup timer/counter 2 as timer
	OCR2 = TF;			// set timer to ca. 51 ms
	TCNT2 = 0;			// clear timer register

	sbi(SFIOR,PSR2);		// Resest Timer Prescaler
	TCCR1B = 0x06;			//start counter
	TCCR2 = 0x07;			//start timer

	ready = 0;
	sbi(TIMSK,OCIE2);		// timer2-compare interrupt on
	sbi(TIFR,OCF2);			// terminate active interrupts, if existing
	sei();				// enable interrupts

	while (ready==0) idle();	// wait until measurement is complete
	n_CNT++;			// increment number of mesurementes executed

	cbi(TIMSK,OCIE2);		// timer2-compare interrupt off
	}

// execute the frequency measuremnt n times
double Measure_M(uint8_t n) {
	double f;
	
	CNT = 0;			// reset the global counter
	n_CNT = 0;			// reset number of measurements executed
	while (n_CNT<n) Measure_1();	// execute n single measurements
	cli();				// no more interrupts
	f=(double)CNT/((double)n*t_gate);// divide total counts by total gate time
	return f;			// that's it
	}

Neben den Deklarationen, die hier nur auszugsweise dargestellt sind, folgt der Interrupt-Behandler für den Timer-2-Interrupt, die Prozedur zur Durchführung einer einzelnen Messung und die Funktion zur Messung der Frequenz basierend auf mehreren Einzelmessungen. Die Konstante TF (Torzeit) wurde so gewählt, daß bei einer zu messenden Frequenz von 1 MHz noch keine Gefahr besteht, daß der Zähler überläuft. Innerhalb etwa 40 ms wird ein Zählerstand von 40000 erreicht, was noch weit genug vom höchstmöglichen Wert 65535 ist.

Tritt der Interrupt auf, so wird als allererstes der Zähler und danach der Timer angehalten. Das Ergebnis des Zählers wird ausgelesen und zum globalen Zähler addiert. Führt man auf diese Art mehrere Messungen aus, so kann die effektive Torzeit auf ganzzahlige Vielfache von etwa 40 ms erhöht werden, was vor allem bei niedrigeren Frequenzen die Genauigkeit erhöht. Danach wird dem Hauptprogramm signalisiert, daß der Interrupt abgearbeitet wurde.

Die Prozedur, die genau eine Messung durchführt, initialisiert im wesentlichen die relevanten Register der beiden Timer/Counter für die nächste Messung und wartet, nachdem timer und counter gestartet wurden, auf das Ende des Interrupts. Dazu wird die Prozedur idle() aufgerufen, in der sinnvolle Dinge durchgeführt werden können. Nach einer Einzelmessung wird der Zähler für die Anzahl der Messungen aktualisiert.

// the timer1-capture interrupt
ISR(TIMER1_CAPT_vect) {
	uint16_t l,h;

	TCCR1B = 0;			// stop timer

	l = TCNT1L;			// read counter and ...
	h = TCNT1H;

	CNT = CNT + l + (h << 8);	// ... add to global counter
	ready = 1;			// notify main program
	}

// measure one time the pulse length of the NE555
void Measure_555_1(void) {
	cli();				// disable all interrupts
	TCCR1A = 0x00;			// prepare timer 1 and ...
	TCCR1B = 0;			// ... stop timer 1

	TCNT1H = 0;			// set timer1 count value to 0
	TCNT1L = 0;

	ready = 0;			// clear the ready status
	sbi(TIFR,ICF1);			// terminate active interrupts, if existing
	sbi(TIMSK,TICIE1);		// timer1-capture Interrupt on

	sbi(SFIOR,PSR10);		// reset prescaler
	TCCR1B=0x01;			// start Timer 1

	cbi(PORTD,5);			// start NE555
	sei();				// enable interrupts
	sbi(PORTD,5);			// return to high level

	while (ready==0) idle();	// wait until ready

	n_CNT++;			// this was one more measurement
	cbi(TIMSK,TICIE1);		// timer1-capture Interrupt off
	}

// execute the pulse length measurement n times
double Measure_555_N(uint8_t n) {
	double t;
	CNT = 0;			// reset the global counter
	n_CNT = 0;			// reset number of measurements executed
	while (n_CNT<n) Measure_555_1();	// execute n single measurements
	cli();				// no more interrupts
	t=(double)CNT/((double)F_CPU*(double)n);	// divide total counts by CPU-frequency and number of measurements
	return t;			// that's it
	}

Die Messung der Frequenz wird von der Funktion Measure_M durchgeführt deren Parameter die Anzahl der Einzelmessungen angibt und deren Rückgabewert die gemessene Frequenz in Hz ist.

8.2 Impulsdauermessung

Die Messung der Kapazität mit dem NE555 basiert darauf, daß die Länge eines Impulses zu messen ist. Während also bei der Frequenzmessung die Torzeit vorgegeben ist und die Anzahl der Impulse in dieser Zeit gezählt werden, ist es bei der Impulsdauermessung umgekehrt. Die Frequenz der zu zählenden Impulse ist fest und die Impulsdauer, die dann der Torzeit entspricht, ist variabel.

Die Deklarationen sind die selben wie für die Frequenzmessung. Daher wird sie hier nicht wiederholt dargestellt. Hier haben wir einen anderen Interrupt-Behandler, der immer dann ausgeführt wird, wenn der Puls des NE555 zurück auf Low wechselt.