Anwendungen

0. Übersicht

Auf dieser Seite möchte ich zeigen, daß das LC-Meter durchaus zu etwas nütze ist. Ich werde von Zeit zu Zeit praktsiche Meßbeispiele zufügen. Das erste Beispiel beschäftigt sich mit der Bestimmung des A_L-Wertes von verschiedenen Kernmaterialien. Im zweiten Beispiel wurde der Kopplungsfaktor eines auf einem Ringkern gewickelten Transformators bestimmt.

1. Beispiel: Der A_L-Wert einiger Ferritkerne

Der A_L-Wert von Kernen (Ringkerne, M-Kerne, E-Kerne, etc.) dient dazu die Anzahl der Windungen zu berechnen, die man auf einen Kern wickeln muß, um eine gewünschte Induktivität zu erhalten. Die Induktivität L errechnet sich gemäß:

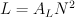
Die Meßvorschrift könnte also sein, eine bestimmte Anzahl von Windungen auf den Kern aufzubringen, die Induktivität zu messen und dann die Meßwerte in die nach N aufglöste Formel einzusetzten:

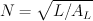
Ich bin einen etwas anderen Weg gegangen. Ich habe zu den Kernen, deren A_L-Wert ich bestimmen wollte, die Induktivität zu jeweils einer, zwei, drei, …, acht Windungen bestimmt und die Werte notiert:

N	L1	L2	L3
1	-	3,2 μH	3,0 μH
2	-	8,8 μH	8,1 μH
3	18 μH	17,3 μH	19,9 μH
4	28 μH	28,4 μH	26,0 μH
5	40 μH	42,6 μH	38,6 μH
6	54 μH	59,8 μH	53,6 μH
7	72 μH	80,3 μH	71,2 μH
8	92 μH	104 μH	91,5 μH

Die drei Spalten L₁, L₂ und L₃ stehen für die gemessenen Induktivitäten eines Amidon Ringkerns FT114-77, eines Kerns der Größe EE25 und eines Kernes der Größe E30. Zum dritten Kern sind mir die Daten völlig unbekannt. Siehe folgende Bilder.

Um aus den Meßreihen auf den A_L-Wert zu kommen, ist es am bequemsten, die Formel an die Meßwerte anzufitten, wobei A_L so lange variiert wird, bis die Summe der Fehlerquadrate minimal wird. Gnuplot [1] hat beispielsweise eine solche Funktion integriert. Das Ergebnis ist dann der A_L-Wert inclusive seines Fehlers. Es hat sich als zweckmäßig herausgestellt, die Formal noch um einen Summanden L₀ zu ergänzen, um konstante Induktivitäten des Meßaufbaus und der Zuleitungskabel zu berücksichtigen. Die Formel, die gefittet wird, ist also:

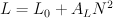
Das Fitergebnis ist in der folgenden Tabelle wiedergegeben:

Kern	AL (gemessen)	AL (lt. Hersteller)	L0
1	1,34 μH/Wdg2 ± 0,6%	1,14 μH/Wdg2 [2]	6,2 μH ± 5%
2	1,59 μH/Wdg2 ± 0,5%	1,90 μH/Wdg2[3]	2,5 μH ± 11%
3	1,40 μH/Wdg2 ± 1%	unbekannt	2,9 μH ± 16%

Die Zuverlässigkeit der A_L-Werte ist sehr gut, was vor allem bedeutet, daß die quadratische Abhängigkeit von der Windungszahl in der Realität hervorragend erfüllt ist. Anders dagegen die absoluten A_L-Werte: Der gemessene Wert des Amidon-Kerns ist rund 18% größer als der Wert den der Herstellers [2] angibt. Bei Kern 2, dem EE25-Kern ist der gemessene Wert 16% kleiner als der Wert nach Herstellerangaben [3]. Allerdings gibt in diesem Fall der Hersteller die Toleranz seines A_L-Werte mit 25% an. Damit liegen die A_L-Werte der ersten beiden Kerne innerhalb der Toleranzgrenzen.

Zum dritten Kern (E30) kann man weiter nichts sagen, weil es keinen Referenzwert gibt. Der wahre A_L-Wert dürfte zwischen 1,12 und 1,87 μH/Wdg² liegen, wenn man 25% Toleranz zugrunde legt. Wahrscheinlich sind die Kerne EE25 und E30 daher nicht aus dem selben Material - zumal der größere E30 einen kleineren A_L-Wert hat, als der kleinere EE25-Kern.

2. Beispiel: Bestimmung der Permeabilität μ_r

Die Induktivität einer Zylinderspule der Länge l und des Wicklungsquerschnitts A mit N Windungen auf einem Kermaterial mit der relativen Permeabilität μ_r läßt sich gemäß

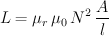
berechnen, wobei μ₀ = 4 π 10^-7 H/m (ca. 1.26x10^-6 H/m) ist. Diese Formel läßt sich leicht nach μ_r auflösen:

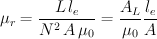
Die Größe l_e steht hier nun für eine effektive Länge der Spule oder - genauer - für die mittlere Länge einer magnetischen Feldlinien, die die Spule durchsetzt. Damit erlangt die Formel prinzipiell Gülrigkeit für beliebige Kernformen. Bei handelsüblichen Kernformen (vor allem bei Ringkerne, E-Kernen und anderen Kernen mit einem geschlossenen magnetischen Kreis) werden die geometrischen Größen l_e und A im Datenblatt mit angegeben (magnetische Formkenngrößen).

Der in der Formel auftretende Quotient aus L und N² kann außerdem durch A_L ersetzt werden. Somit können die im vorherigen Beispiel bestimmten A_L-Werte hier direkt weiterverwendet werden, um auch die relative Permeabilität zu erhalten. Das Beispiel wird sich also wieder auf die drei oben erwähnten Kerne (Amidon FT114-77, ein EE25 und ein E30) beziehen. Die folgende Tabelle zeigt das Ergebnis der einfachen Rechnung.

Kern	A	le	AL (gemessen)	AL (laut Hersteller)	μr (gemessen)	μr (laut Hersteller)
1	0,375 cm2	7,42 cm	1,34 μH/Wdg2	1,14 μH/Wdg2	2110	2050 [2]
2	0,525 cm2	5,75 cm	1,59 μH/Wdg2	1,90 μH/Wdg2	1390	ca. 2000 [4]
3	0,60 cm2	6,7 cm	1,40 μH/Wdg2		1240

Die Permeabilität des Amidon-Kernes wurde recht gut bestätigt. Die des EE25 Kernes weicht doch erheblich vom Wert ab, den das Material erwarten läßt. Interessanterweise hat der Kern mit dem umbekannten Material eine Permeabilität, die erstaunlich dicht am Meßwert des EE25-Kernes liegt. In Anbetracht der Abweichungen zu den Herstellerangaben ist diese Gleichheit natürlich mit Vorsicht zu interpretieren.

3. Beispiel: Der Kopplungsfaktor zweier Wicklungen auf einem Ferrit-Ringkern

Auf einen Amidon Ringkern FT114-77 [2] wurden als Sekundärwicklung etwas über 90 Windungen eines 0,15 mm CuLL-Drahtes - Windung an Windung - aufgebracht. Die Wicklung belegt damit etwa die Hälfte des Kerns. Mittig auf der freien Hälfte wurden 8 Windungen - ebenfalls Windung an Windung - eines 0,8 mm CuL-Drahtes als Primärwicklung aufgebracht. Ein leere und ein bewickelter Kern ist im folgenden Bild dargestellt.

Der Versuch, diesen Transformator als Durchflußwandler zu benutzen, schlug allerdings fehl, weil es im Ausschaltmoment auf der Primärseite sehr energiereiche Spannungsspitzen gab, die das angeschlossene Snubber-Netzwerk zu stark belasteten. Dieser Effekt ist ein deutliches Indiz für eine zu hohe Streuinduktivität. Das heißt, es steht zu befürchten, daß der Kopplungsfaktor nicht nahe genug bei 1 ist.

Wie sich der Kopplungfaktor k messen läßt, ist hier erklärt. Hier nochmal zusammenfassend die Formel:

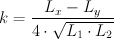
Gemessen werden jeweils die einzelnen Induktivitäten der Wicklungen auf dem Kern (L₁, L₂) sowie die resultierende Induktivität, wenn man beide Wicklungen in Reihe schaltet (L_x) und wenn man eine Wicklung der Reihenschaltung umpolt (L_y). Hier die Meßwerte:

Messung von	Messwert
L1	110 μH
L2	13,8 mH
Lx	16,3 mH
Ly	11,6 mH

Eingesetzt in die Formel ergibt sich ein Kopplungsfaktor von k=0,95, was deutlich kleiner als 1 ist. Damit hat sich der Verdacht erhärtet, daß zumindest diese Art des Bewickelns eines Ferrit-Ringkernes eher ungeeignet ist.

Referenzen und Links

• [1]: Die (englische) Gnuplot-Homepage
• [2]: Amidon Deutschland
• [3]: Spulenbausatz 516678 - 62 (Conrad)
• [4]: Eigenschaften des Werkstoffes Manifer 196