Messung der Induktivität Lx und der parasitären Kapazität Ly
| (%i1) | kill(all)$ |
Bestimmung der Induktivität Lx und der parasitären Kapazität Cy mittels zweier Messungen.
Erste Messung:
f1 wird gemessen; die aktiven Komponenten im Schwingkreis sind Lx, Cy und C13
Zweite Messung:
f2 wird gemessen; die aktiven Komponenten im Schwingkreis sind Lx, Cy, C13 und zusätzlich C15
C13 und C15 werden als bekannt vorausgesetzt; f1 und f2 werden gemessen wobei nur im ersten Fall C15 zugeschaltet ist
Setzt man die Bauteilewerte in die Thomsonsche Schwingungsformel für den ersten Fall ein, so erhält man
für f1 folgenden Ausdruck A1:
| (%i1) | A1:1/(2*%pi*sqrt(Lx*(Cy+C13))); |
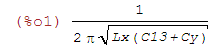
Analog für den zweiten Fall mit zugeschalteter Kapazität C15 erhält man für f2 den Ausdruck A2
| (%i2) | A2:1/(2*%pi*sqrt(Lx*(Cy+C13+C15))); |
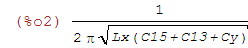
Wir haben also zwei Gleichungen (eine für f1, eine andere für f2) und zwei Unbekannte (Lx, Cy).
Zur Lösung ist es allerdings zweckmäßig, mit den quadrierten Thomsonschen Schwingungsformeln zu arbeiten.
Die Quadrate der beiden oberen Ausdrücke A1 und A2 sehen dann wie folgt aus:
| (%i3) | A3: A1^2; |
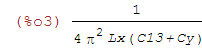
| (%i4) | A4:A2^2; |
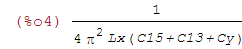
Diese beiden Ausdrücke für f1^2 und f2^2 kann man jetzt leichter lösen:
| (%i5) | solve([f1^2=A3,f2^2=A4],[Lx,Cy]); |
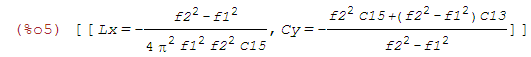
Jetzt kann man noch ein wenig umformen und vereinfachen; aber im prinzip ist dies bereits die fertige Lösung.
Die Minus-Vorzeichen wir man dadurch los, daß man für Lx im Zähler die Differenz der Frequenzquadrate umdreht;
analog im Nenner von Cy.
Außerdem kann man Cy in zwei Summanden aufteilen wobei sich beim zweiten Summanden die Differenzen der Quadrate der
Frequenzen kürzen und C13 - allderding mit einem Minus-Zeichen - übrig bleibt.